

Design Center
DIGITAL IMAGE PROCESSING
Digital image processing is known to be tough for budding engineers. It is because the majority of the books regarding DIP are dealing with mathematical equations, without trying to make us understand the real concept. This article will show how simple is the basic concepts of DIP.
Image Processing Based on Convolution:
The science of manipulating digital images often involves the mathematical operation called convolution. Convolution is one of the basic building blocks of DIP. Convolution is defined mathematically as follows:
Image Processing Based on Convolution:
The science of manipulating digital images often involves the mathematical operation called convolution. Convolution is one of the basic building blocks of DIP. Convolution is defined mathematically as follows:
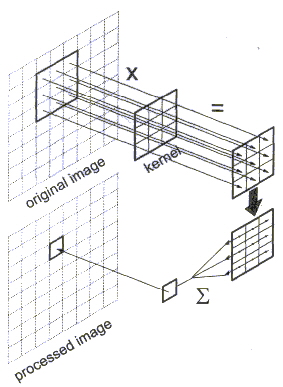
Where I(x) is the input, g(x) is the result, and h(x) is called the convolution kernel. When applied to digital images, this integral equation results in essentially just shifting and adding gray scale values. Convolution is a straightforward operation that should be understood by all professionals. Figure illustrates convolution as it applies to digital images.
The functional form of the convolution kernel h(x) (i.e., its shape when plotted) can have a profound influence on the appearance of the processed image. Let us take the example of a simple 3x3 convolution kernel, and examine how the nine values that result can be manipulated to achieve different effects. The following kernel is called a delta function, and convolving with it does not change an image in any way:
The functional form of the convolution kernel h(x) (i.e., its shape when plotted) can have a profound influence on the appearance of the processed image. Let us take the example of a simple 3x3 convolution kernel, and examine how the nine values that result can be manipulated to achieve different effects. The following kernel is called a delta function, and convolving with it does not change an image in any way:
The concept of discrete convolution as used in digital image processing is illustrated. A 3 x 3 pixel region of the original image is multiplied by a 3 x 3 convolution kernel. The nine products of this multiplication are summed, and the result is placed in the pixel in the processed image corresponding to the center of the 3 x 3 region on the original image. The convolution operation moves across the entire image, pixel by pixel.
0 0 0
0 1 0
0 0 0
Shifting operation of image:
An entire image can be shifted one pixel to the left by the following kernel:
0 0 0
1 0 0
0 0 0
Blurring operation of image:
When all the values in the kernel are positive and non-zero, the kernel blurs an image. For example, the following kernel smoothes some of the noise in an image but also reduces its resolution somewhat:
1 1 1
1 1 1
1 1 1
0 0 0
0 1 0
0 0 0
Shifting operation of image:
An entire image can be shifted one pixel to the left by the following kernel:
0 0 0
1 0 0
0 0 0
Blurring operation of image:
When all the values in the kernel are positive and non-zero, the kernel blurs an image. For example, the following kernel smoothes some of the noise in an image but also reduces its resolution somewhat:
1 1 1
1 1 1
1 1 1
Smoothing with a 3 x 3 kernel produces a subtle blurring effect that is not well appreciated on an image at textbook resolution. However, the convolution can be performed using a larger kernel (e.g., 11 X 11) to achieve substantial blurring effects that are easy to see.
When the 3x3 kernel containing all ones is convolved with an image, the sum of all the gray scale values in the resulting image is nine times greater than the sum of all the gray scale values in the original image. To correct for this, the resulting image is divided by 9 (pixel by pixel). Another way to perform this normalization is to divide all the kernel values by 9 before convolution is performed:
1/9 1/9 1/9
1/9 1/9 1/9
1/9 1/9 1/9
Sharpening operation of image:
When the kernel contains both positive and negative numbers, the image, instead of being smoothed, will be sharpened.
-1 -1 -1
-1 9 -1
-1 -1 -1
An image that has been smoothed with the use of a blurring kernel can be subtracted from the original image to produce a harmonized image. The original image contains both low- and high-frequency components, but in the blurred image high-frequency structures are dampened. The difference image tends to reduce low-frequency components in the image, accentuating the high-frequency structures (edges).
Deconvolution:
Convolution in principle can be undone by deconvolution; however, a noise penalty often occurs. Deconvolution is essentially the same thing as convolution, except that the shape of the deconvolution kernel is designed to reverse the effects of a convolution kernel or physical process. For example, if an image is convolved with a kernel K, and then is convolved with its inverse K-1 (i.e., deconvolved), the original image will be reproduced.
Median Filtering:
Convolution with a 3 X 3 kernel of all ones is a process of averaging nine adjacent pixels and storing the average value in the center pixel of the new image. The average is affected by outlying values (high or low), whereas the median is the middle value and is unaffected by outliers.
One last word:
Anyone who knows C or C++ programming can easily implement these Digital Image Processing techniques.
Reference:
"Digital Radiography"
When the 3x3 kernel containing all ones is convolved with an image, the sum of all the gray scale values in the resulting image is nine times greater than the sum of all the gray scale values in the original image. To correct for this, the resulting image is divided by 9 (pixel by pixel). Another way to perform this normalization is to divide all the kernel values by 9 before convolution is performed:
1/9 1/9 1/9
1/9 1/9 1/9
1/9 1/9 1/9
Sharpening operation of image:
When the kernel contains both positive and negative numbers, the image, instead of being smoothed, will be sharpened.
-1 -1 -1
-1 9 -1
-1 -1 -1
An image that has been smoothed with the use of a blurring kernel can be subtracted from the original image to produce a harmonized image. The original image contains both low- and high-frequency components, but in the blurred image high-frequency structures are dampened. The difference image tends to reduce low-frequency components in the image, accentuating the high-frequency structures (edges).
Deconvolution:
Convolution in principle can be undone by deconvolution; however, a noise penalty often occurs. Deconvolution is essentially the same thing as convolution, except that the shape of the deconvolution kernel is designed to reverse the effects of a convolution kernel or physical process. For example, if an image is convolved with a kernel K, and then is convolved with its inverse K-1 (i.e., deconvolved), the original image will be reproduced.
Median Filtering:
Convolution with a 3 X 3 kernel of all ones is a process of averaging nine adjacent pixels and storing the average value in the center pixel of the new image. The average is affected by outlying values (high or low), whereas the median is the middle value and is unaffected by outliers.
One last word:
Anyone who knows C or C++ programming can easily implement these Digital Image Processing techniques.
Reference:
"Digital Radiography"